От редакции:

Что мы воспринимаем как неотъемлемо принадлежащее зиме?

Если говорить о погоде, то каждый ребенок (а с ним и взрослые, но это секрет!) ждет, когда выпадет снег. Ждем, когда однажды, выглянув в окно, обнаружим, что мир изменился за одну ночь — все обновилось, стало таким чистым и белым. «Белоснежным», — говорим мы.

Дети ждут снега, чтобы кататься с горы до тех пор, пока ботинки не промокнут насквозь, а щеки не начнут пылать как две розы.

Взрослых привлекает то, что мир выглядит обновленным. Их восхищает способность природы покрыть за одну ночь огромнейшее пространство таким ровным, гладким слоем вещества (попробуйте это сделать — не так-то просто покрыть, например, ровным слоем цемента десять квадратных метров на полу вашей кухни!).

Если этот взрослый — художник, он может быть вдохновлен на написание картины. Если он — поэт, то родится стихотворение.

А если он ученый?

Современный ученый скажет приблизительно так: снежинка — это маленькое упорядоченное скопление кристалликов льда, имеющее шестиугольную форму. Также он может добавить, что оно обладает симметрией шестого порядка, что форма обусловлена структурой кристаллической решетки и т.д.

А если ученый, направивший внимание на снежинку, из 17-го века? Тогда он может написать трактат о снежинках, где в непостижимой (увы!) современному человеку форме он выражает себя не только как исследователь кристалла, но как геометр и философ, внимательный наблюдатель растений и животного мира, физик и поэт… Словом, как представитель того времени, когда, будучи ученым, нельзя было ограничиться одной областью и не быть поэтом и художником.

Славному придворному советнику
Его императорского величества
господину Иоганну Маттею Вакгеру фон Вакенфельсу,
золотому рыцарю и прочая, покровителю наук и философов,
господину моему благодетелю

Поскольку мне доподлинно известно, сколь сильно ты любишь Ничто не по причине его незначительной ценности, а скорее как прелестную забаву шаловливо щебечущего воробья, то нетрудно догадаться, что любой дар будет для тебя тем приятнее и желаннее, чем сильнее он будет походить на Ничто.

Ведь в любом случае для того, чтобы размышления о ничтожном доставили тебе удовольствие, оно должно быть и малым, и почти неощутимым, то есть почти Ничем. В природе встречается великое множество таких вещей, но между ними имеются различия. Вспомни хотя бы об одном из атомов Эпикура: такой атом и есть Ничто. Разумеется, тебе и прежде случалось получать от меня Ничто. Итак, нас будут интересовать элементы, то есть самое малое из того, что есть в каждом предмете…

Погруженный в подобного рода размышления, я перехожу мост, терзаемый стыдом за свою невежливость: ведь непрестанно играя на одной и той же струне (предлагая Ничто или находя нечто мало отличающееся от него, но не дающее пищу твоему острому разуму), я оставил тебя без новогоднего подарка! И тут мне подворачивается удобный случай: водяные пары, сгустившись от холода в снег, выпадают снежинками на мою одежду, все, как одна, шестиугольными с пушистыми
лучами. Клянусь Гераклом, вот вещь, которая меньше любой капли, имеет форму, может служить долгожданным новогодним подарком любителю Ничего и достойна математика, обладающего Ничем и получающего Ничто, поскольку падает с неба и таит в себе подобие шестиугольной звезды!

Ее необходимо поскорее передать моему покровителю, пока мой крохотный подарок еще тверд и не обратился в Ничто под действием тепла, исходящего от тела…

…Итак, прими сей дар, который очень походит на Ничто, и сделай серьезную мину, если ты благоразумен, и затаи дыхание, чтобы не оказалось, что ты и впрямь получаешь Ничто. Подобно Сократу, я вынужден говорить о блошиных прыжках: о том, почему снежинки, прежде чем убиться в крупные хлопья, падают шестиугольниками и пушистыми, как перышки с шестью лучами.

Но шутки в сторону — займемся делом. Поскольку всякий раз, когда начинает идти снег, первые снежинки имеют форму шестиугольной звезды, то на то должна быть определенная причина. Ибо если это случайность, то почему не бывает пятиугольных или семиугольных снежинок, почему всегда падают шестиугольные, если только они от соударений не утрачивают форму, не слипаются во множестве, а падают редко и порознь? Когда я недавно рассуждал с кем-то на эту тему, то мы сошлись прежде всего на том, что причину следует искать не в веществе, а в действующем начале. Ведь вещество снега — это пар. Выделяясь под действием какого-то своего тепла из Земли, пар становится сплошным и как бы жидким. Следовательно, ни на какие звездочки пар не разделен…

…Но коль скоро установлено, что причина свойственной снегу шестиугольный формы кроется в действующем начале, то позволительно спросить, каково это действующее начало, как оно действует, является ли форма искони присущей телу или приобретается под влиянием внешних воздействий, принимает ли материал шестиугольную форму в силу необходимости или по своей природе и что следует считать врожденным: воплощенный в шестиугольном архетип, красоты или знание цели, к которой приводит эта форма?…

…Если спросить у математиков, в каком порядке построены пчелиные соты, то они ответят, что в шестиугольном. <…> Пчелы от природы наделены инстинктом, позволяющим строить соты именно такой, а не другой формы. Этот архетип заложен в них творцом. Здесь ни при чем ни материал, ни воск, ни тельца пчел, ни рост.

Плоскость можно покрыть без зазоров лишь следующими фигурами: равносторонними треугольниками, квадратами и правильными шестиугольниками. Среди этих фигур [если их вписать в одну окружность] правильный шестиугольник покрывает наибольшую площадь. Пчелы же стремятся строить как можно более вместительные соты, чтобы запасти побольше меда. Те же соображения применимы и к трехмерному пространству…

Наоборот, если спросят, почему у всех деревьев и кустарников или по крайней мере у большинства из них цветы, распускаясь, приобретают пятиугольную форму, то есть имеют по пяти лепестков
(у яблонь и груш эта форма цветков соответствует также строению плода, основанному на числе пять или на родственном числе 10, поскольку внутри плода семена находятся в пяти камерах и заключены между 10 перегородками, что также наблюдается у огурцов и тому подобных овощей и фруктов), то я отвечу, что здесь рассуждения о красоте и свойствах фигуры, в которых проявляется душа растения, были бы вполне уместны…

Если бы мы вздумали исследовать, откуда у снега берется эта (шестиугольная) фигура, и отделили бы внешние причины от внутренних, то среди внешних причин нам прежде всего встретился бы холод. Во всяком случае, сгущение водяных паров происходит под влиянием холода, а ведь именно при сгущении пар превращается в звездообразные фигуры. Следовательно, можно считать, что возникновение звездообразных фигур обусловлено холодом. Это, в свою очередь, наводит на новые размышления о том, не является ли холод неким природным началом, чем-то вроде тепла медиков? Ведь насколько можно судить, холод — это не просто отсутствие тепла, поскольку недостающее качество не обладает разумом, создателем шестиугольной формы, и не способно производить какие-либо действия. Но, чтобы не смешивать вопросов, оставим сгущение паров холоду…

…Имеются основания считать, что отдельные капли могут выстраиваться в определенном порядке сами, без прикосновения извне. Ведь если бы форма отдельных капель определялась относительным расположением и касаниями множества капель, то все звезды по форме были бы почти одинаковыми, в то время как в действительности они значительно отличаются по величине.
И даже в строении многих звездочек можно заметить много необычного.

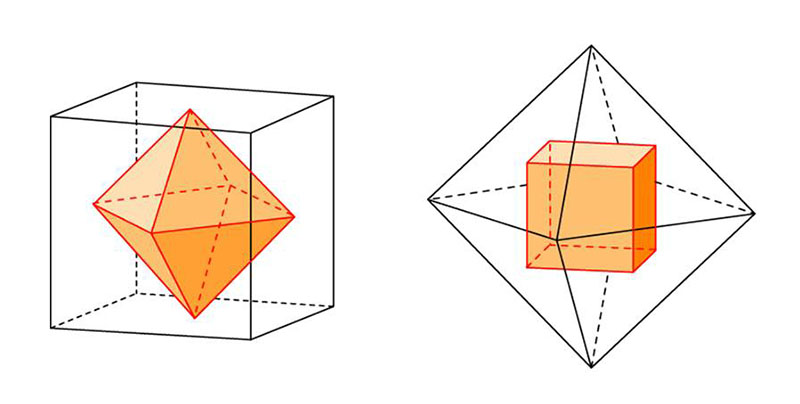
…Мельчайшая частица пара, отделившаяся от общей массы, прежде всего принимает форму куба, <…> или форму его спутника октаэдра. Кроме того, начинает действовать необходимость, обусловленная свойствами сваленных в кучу одинаковых по своим размерам шариков. Ведь шарики перемешаны и в точках касания выглядят, как заготовки кубов и октаэдров. Почему октаэдры встречаются чаще, чем кубы? Может быть, потому что куб возникает при расширении, а октаэдр при сжатии? Ведь и вещество, и согревающая сила при враждебном нападении холода сжимаются. Откуда же известно, что одна фигура возникает при расширении, а другая при сжатии? Это следует из того, что у куба все его восемь вершин обращены наружу, а у октаэдра вокруг центра имеется такое же число вершин, обращенных внутрь. Ведь если восемь вершин куба отсечь равными гранями и, повернув отрезанные части, поместить их внутрь оставшейся части куба, то получится именно октаэдр. Таким образом, обе фигуры можно разделить так, что число вершин куба возрастет до восьми, а число вершин октаэдра уменьшится до шести.

Гранильщики драгоценных камней утверждают, что в алмазах встречаются естественные октаэдры совершеннейшей и изящнейшей «формы. Если это так, то свидетельство ювелиров существенно подкрепляет сказанное выше. Ведь жизненная сила, придавшая в недрах Земли алмазам форму октаэдров, почерпнутую из сокровеннейших глубин своей природы, выйдя из Земли вместе с паром, придала образовавшемуся из пара снегу ту же самую форму…

Далеко ли я, глупец, ушел, если, намереваясь подарить тебе почти Ничто, почти Ничего не делая, я умудрился из этого почти Ничто сотворить почти целый мир со всем, что в нем находится? Не я ли, отправляясь затем от крохотной души самого маленького из живых существ, трижды обнаруживал душу самого большого из живых существ — Земного шара — в атоме снега?..

…Пока я писал эти строки, снова пошел снег, причем еще пуще прежнего. Я прилежно принялся разглядывать снежинки. Все они были с прямыми лучами, но двух родов. Одни снежинки были очень маленькими, с различным числом торчащих кругом лучей, голых, лишенных опушки и полосочек и очень тонких. В центре лучи сходились к шарику несколько большей величины. Таких снежинок было больше всего. Среди них были разбросаны более редкие снежинки второго рода — шестиугольные звездочки, ни одна из них, ни пока она падала, ни после того, как опускалась на землю, не напоминала по форме другую. Пушинки у звездочек располагались в одной плоскости с лучами. Седьмой, более короткий луч торчал вниз, как корень, на который могли опускаться падающие снежинки, и, опустившись, держались на нем некоторое время. Это обстоятельство не ускользнуло от меня во время предыдущих моих наблюдений, но было неверно истолковано мной так, будто три диаметра, образующие остов снежинки, не лежат в одной плоскости. Поэтому то, о чем я говорил прежде, ничуть не менее близко к Ничему, чем то, о чем я поведал тебе только что.

Снежинки первого рода, напоминающие по форме градины, как мне кажется, возникают из пара, почти лишенного теплоты и начавшего сгущаться в водяные капли. Поэтому они круглые, некрасивы с виду, лишены формообразующей силы, а их центральные ядра усажены со всех сторон лучами по той же причине, по которой на окне образуется иней…

Что касается снежинок второго рода, имеющих форму звездочек, то в них нельзя усмотреть ни куба или октаэдра, ни соприкосновения капель, поскольку эти звездочки падают плоскими, а не в виду пересекающихся диаметров, как я предполагал выше.

Хотя и в данном случае формообразующая сила остается на месте и по-прежнему предопределяет форму снежинок, снова возникает вопрос о выборе формы. Прежде всего, почему снежинки плоские? Может быть, выше я безосновательно лишил плоскость формообразующей силы? Ведь все цветы имеют форму правильных плоских пятиугольников, а не объемного додекаэдра. Причина, порождающая плоскую фигуру, могла бы состоять в том, что холод соприкасается с теплым паром
вдоль некоторой плоскости, причем не весь пар оказывается окруженным холодом равномерно. Тогда образовывались бы звездочки, но выпадали бы градины.

Но почему возникает именно правильный шестиугольник? Не потому ли, что из всех правильных фигур шестиугольник является первой, из которой нельзя собрать объемное тело? Ведь и равносторонний треугольник, и квадрат, и правильный пятиугольник тела образуют. Может быть, потому, что правильными шестиугольниками можно покрыть плоскость без единого зазора? Но тем
же свойством обладают и равносторонний треугольник, и квадрат. Может быть, потому, что из всех правильных плоских фигур, способных сплошь, без единого зазора покрывать плоскость, правильный шестиугольник ближе всего подходит к кругу? Может быть, причину следует искать в различии между силой, вызывающей бесплодие, и другой, плодотворящей силой, считая, что первая порождает правильные пятиугольники, а вторая — равносторонние треугольники и правильные шестиугольники? Может быть, наконец, сама формообразующая природа в своей глубочайшей сущности сопричастна правильному шестиугольнику?..

…Что же касается цветов с шестью лепестками, то из них не вырастет ничего, кроме семян в сухой оболочке, и плод сидит прямо на цветке. Может быть, различие состоит в том, что цветы с шестью лепестками не встречаются у деревьев и кустарников, а лишь у трав и в особенности у луковичных растений? Может быть, кто-нибудь другой изучит соки растений, чтобы выяснить, не в них ли кроется различие между формами цветов?

…Вполне возможно, что формообразующая сила действует по-разному от различного содержания влаги. В купоросе часто встречаются кристаллы куборомбической формы, в селитре форма кристаллов иная. Поэтому химики должны сказать, нет ли в снеге какой-нибудь соли, какого рода эта соль и какие фигуры она может порождать. Постучавшись в дверь химии, я вижу, сколько еще мне осталось сказать, чтобы постичь подлинную природу данного явления, и поэтому предпочитаю услышать, что думаешь по этому поводу ты, проницательнейший из мужей, нежели утомлять тебя своими догадками.

Вот и все.

Из журнала «Химия и жизнь», №12, 1983

Опубликовано в журнале «Дитина», №9-10, 2003

Источник фото